DBSCAN vs. Other Algorithms
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a powerful clustering algorithm, especially suited for data with clusters of arbitrary shapes and the presence of noise. However, it's not always the best choice for every clustering problem. This article compares DBSCAN with other popular clustering algorithms, including K-Means, Agglomerative Hierarchical Clustering, Spectral Clustering, and t-SNE, to help you decide which method is best suited for your specific needs.
1. DBSCAN vs. K-Means Clustering
Overview of K-Means:
K-Means is a centroid-based clustering algorithm that partitions data into clusters, where each cluster is represented by the mean (centroid) of its points. Unlike DBSCAN, K-Means requires the number of clusters to be defined beforehand and assumes clusters to be roughly spherical.
Key Differences:
| Feature | DBSCAN | K-Means |
|---|---|---|
| Cluster Shape | Detects clusters of arbitrary shapes | Assumes spherical clusters |
| Number of Clusters | Automatically detects based on density | Must be pre-defined |
| Handling Noise | Explicitly handles noise (outliers) | Poor handling of noise |
| Distance Metric | Uses a distance parameter (ε) to define clusters | Typically uses Euclidean |
| Scalability | Not as scalable for very large datasets | Scales well with large data |
Example:
- When to use DBSCAN: Use DBSCAN when clusters have arbitrary shapes, and you want to detect noise or outliers in spatial data.
- When to use K-Means: Use K-Means when you know the number of clusters, the clusters are roughly spherical, and the data has few outliers.
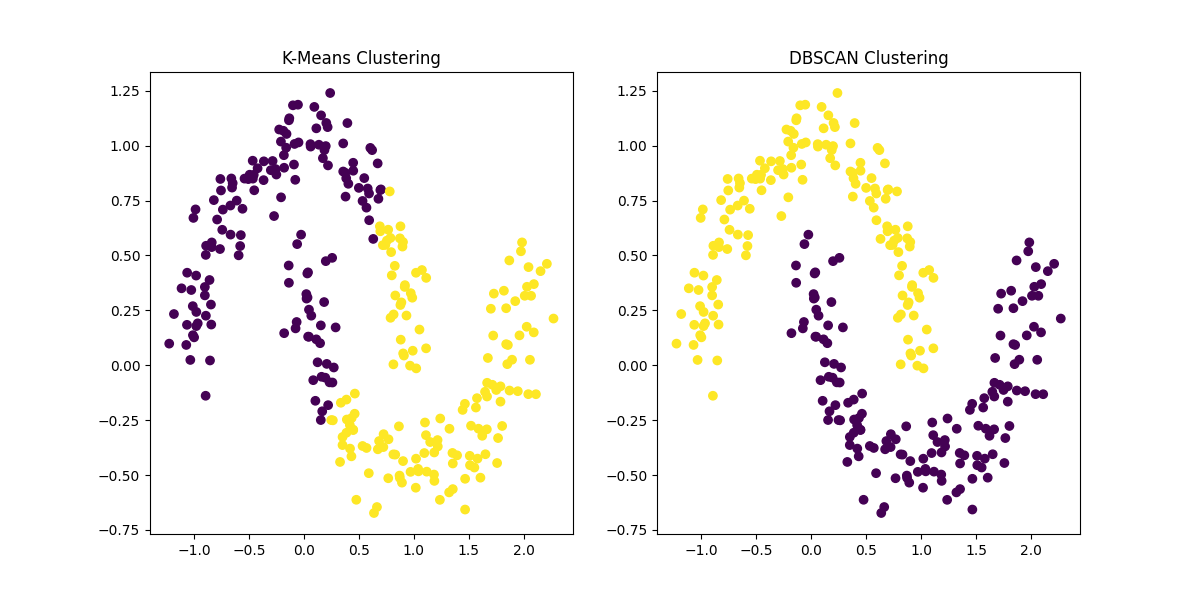
Figure 1: Comparison of K-Means Clustering and DBSCAN on a dataset with two interlocking half-moon shapes. K-Means assumes spherical clusters and struggles to identify the correct clusters, while DBSCAN accurately identifies the non-convex clusters and handles noise.
2. DBSCAN vs. Agglomerative Hierarchical Clustering
Overview of Agglomerative Hierarchical Clustering:
Agglomerative Hierarchical Clustering is a bottom-up clustering method that builds a hierarchy of clusters by merging or splitting them based on a distance metric. Unlike DBSCAN, it does not require the specification of a distance parameter but instead builds a hierarchy that can be visualized as a dendrogram.
Key Differences:
| Feature | DBSCAN | Hierarchical Clustering |
|---|---|---|
| Number of Clusters | Automatically detects based on density | Can be chosen by cutting the dendrogram |
| Cluster Shape | Detects clusters of arbitrary shapes | Works with clusters of arbitrary shapes |
| Scalability | Not as scalable for very large datasets | Computationally expensive for large datasets |
| Distance Metric | Uses a distance parameter (ε) | Can use various distance metrics |
| Cluster Hierarchy | No hierarchy | Builds a hierarchy of clusters (dendrogram) |
Example:
- When to use DBSCAN: Use DBSCAN when you expect clusters of varying shapes and sizes, especially in spatial data.
- When to use Agglomerative Clustering: Use Agglomerative Clustering when the dataset is small to medium-sized, and you are interested in a hierarchy of clusters or cannot determine the number of clusters beforehand.
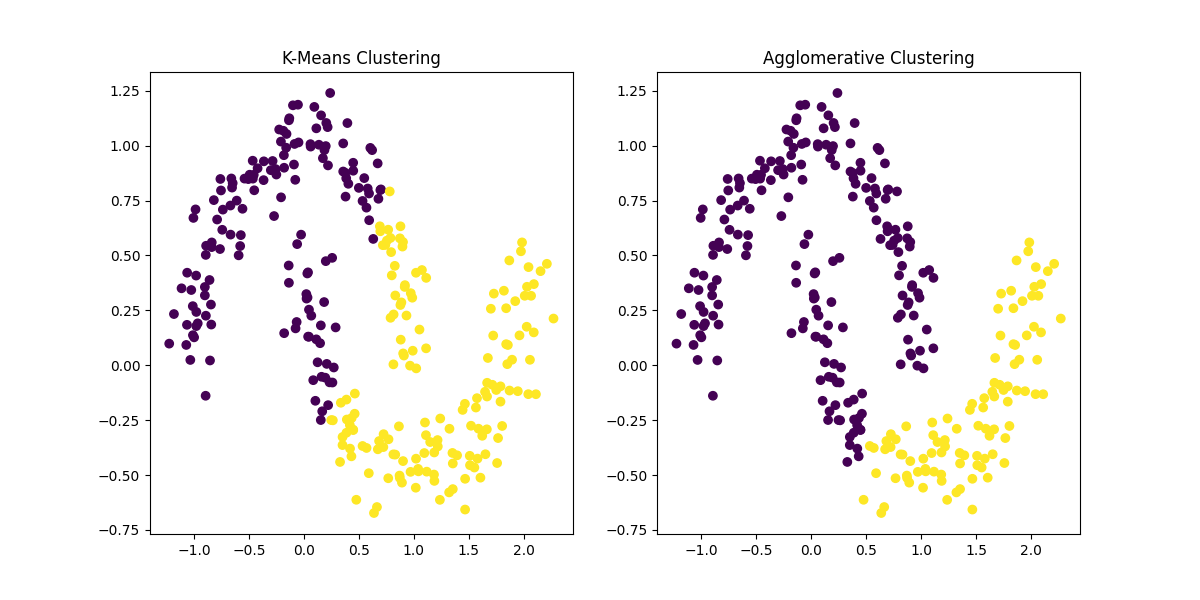
Figure 2: Comparison of K-Means Clustering and Agglomerative Hierarchical Clustering on the same dataset. While K-Means struggles with non-convex shapes, Agglomerative Clustering can detect clusters of arbitrary shapes, although it may be computationally more expensive for larger datasets.
3. DBSCAN vs. Spectral Clustering
Overview of Spectral Clustering:
Spectral Clustering is a graph-based clustering algorithm that uses the eigenvalues of a similarity matrix to reduce dimensionality before clustering. Unlike DBSCAN, which relies on density, Spectral Clustering is particularly useful for identifying clusters with complex structures and shapes.
Key Differences:
| Feature | DBSCAN | Spectral Clustering |
|---|---|---|
| Cluster Shape | Detects clusters of arbitrary shapes | Handles complex, non-convex clusters |
| Number of Clusters | Automatically detects based on density | Can determine clusters based on eigenvalue gaps |
| Dimensionality | Operates in raw data space | Works on reduced dimensionality from eigenvalues |
| Scalability | Not as scalable for very large datasets | Less scalable, requires eigen decomposition |
Example:
- When to use DBSCAN: Use DBSCAN for clustering spatial data or when you expect clusters of arbitrary shapes with noise.
- When to use Spectral Clustering: Use Spectral Clustering for complex clustering tasks where the cluster boundaries are non-linear or non-convex, such as image segmentation or graph-based data.
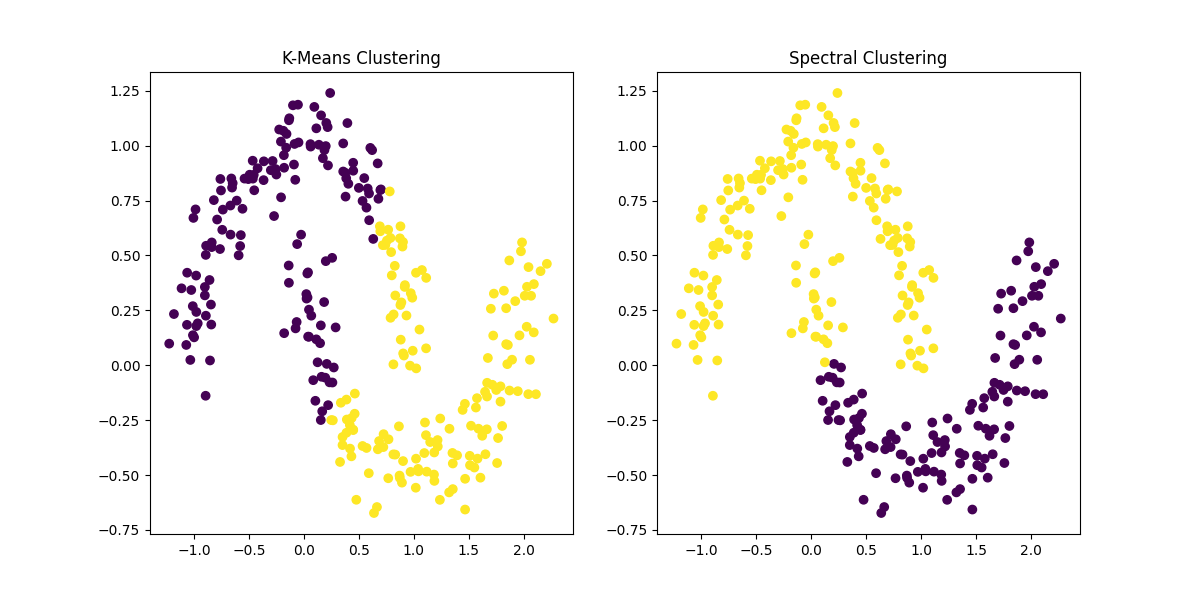
Figure 3: Comparison of K-Means Clustering and Spectral Clustering. Spectral Clustering effectively captures the complex, non-convex shapes in the data that K-Means fails to detect, making it more suitable for datasets with intricate cluster structures.
4. DBSCAN vs. t-SNE (t-Distributed Stochastic Neighbor Embedding)
Overview of t-SNE:
t-SNE is primarily a dimensionality reduction technique used for visualizing high-dimensional data in a lower-dimensional space (2D or 3D). While not explicitly a clustering algorithm like DBSCAN, t-SNE is often used to visualize clusters.
Key Differences:
| Feature | DBSCAN | t-SNE |
|---|---|---|
| Purpose | Clustering | Visualization |
| Dimensionality | Operates in raw data space | Reduces dimensionality for visualization |
| Number of Clusters | Automatically detects based on density | Does not explicitly define clusters |
| Interpretation | Provides hard cluster assignments | Provides a visual map of data relationships |
| Scalability | Not as scalable for very large datasets | Computationally expensive for large datasets |
Example:
- When to use DBSCAN: Use DBSCAN when you need to identify clusters with arbitrary shapes and detect noise.
- When to use t-SNE: Use t-SNE when you want to visualize high-dimensional data and explore patterns visually. t-SNE helps in exploring data relationships, even though it doesn’t give explicit cluster memberships.
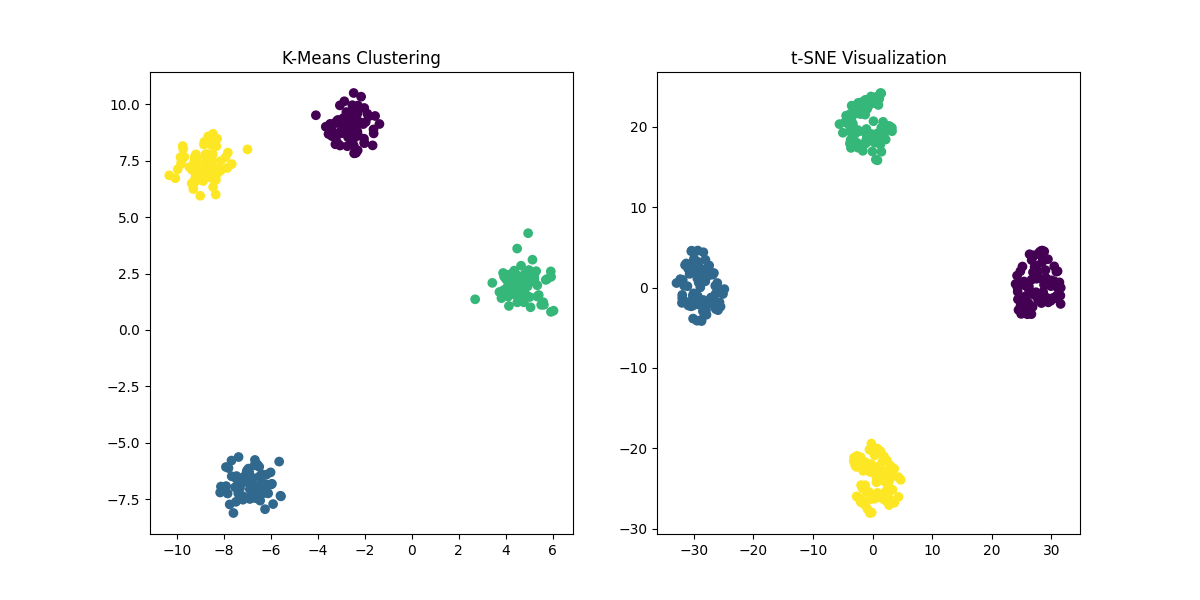
Figure 4: Comparison of K-Means Clustering and t-SNE. While K-Means clusters the data based on predefined centroids, t-SNE provides a low-dimensional representation of the data that helps in visualizing the structure of high-dimensional data.
5. DBSCAN vs. UMAP (Uniform Manifold Approximation and Projection)
Overview of UMAP:
UMAP is another dimensionality reduction technique that, like t-SNE, is often used for visualizing clusters. UMAP is generally faster than t-SNE while preserving more of the global structure in the data.
Key Differences:
| Feature | DBSCAN | UMAP |
|---|---|---|
| Purpose | Clustering | Dimensionality Reduction & Visualization |
| Dimensionality | Operates in raw data space | Reduces dimensionality to 2D or 3D |
| Cluster Assignment | Hard clusters | Provides a visual representation of clusters |
| Scalability | Not as scalable for very large datasets | More scalable than t-SNE, but less than DBSCAN |
Example:
- When to use DBSCAN: Use DBSCAN for clustering tasks where noise detection and arbitrary cluster shapes are important.
- When to use UMAP: Use UMAP when you want to reduce high-dimensional data into a low-dimensional space for visualization, particularly when you need to preserve both local and global data structure.
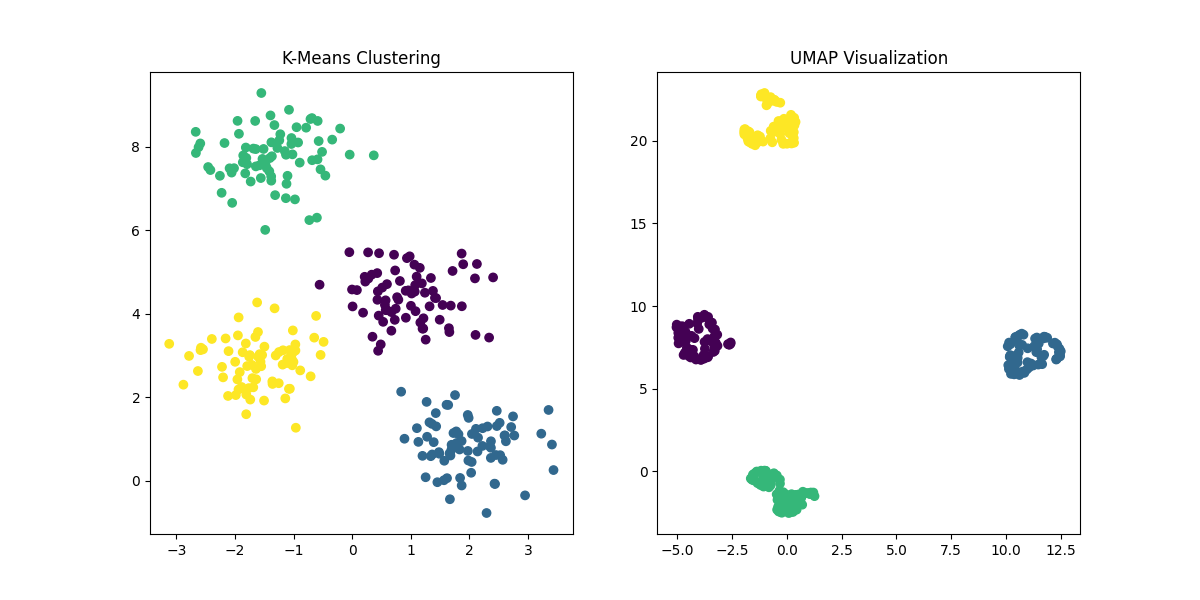
*Figure 5: Comparison of K-Means Clustering and UMAP. UMAP, like t-SNE, is used
for dimensionality reduction and visualization, preserving more of the global structure compared to t-SNE, and providing an alternative way to explore the data's intrinsic patterns.*
Conclusion
DBSCAN is an effective clustering algorithm for identifying clusters of arbitrary shapes and handling noise, making it particularly suitable for spatial data analysis. However, depending on the specific characteristics of your dataset, other algorithms such as K-Means, Agglomerative Hierarchical Clustering, Spectral Clustering, t-SNE, or UMAP may be better suited.
- Use DBSCAN: When you expect clusters of arbitrary shapes, and noise/outliers need to be detected.
- Use K-Means: When the number of clusters is known, clusters are spherical, and the dataset is relatively large.
- Use Agglomerative Clustering: When you need hierarchical relationships or cannot pre-define the number of clusters.
- Use Spectral Clustering: When clusters have complex, non-convex shapes, or in graph-based data.
- Use t-SNE/UMAP: When you need to visualize high-dimensional data and explore relationships in a lower-dimensional space.
Each of these algorithms has strengths and weaknesses, and the choice depends on the nature of your data and your specific goals. Understanding the key differences between these methods will help you select the best algorithm for your project.