Applications of Spectral Decomposition in Clustering

Spectral decomposition is a powerful mathematical tool in linear algebra with wide-ranging applications in clustering algorithms. By breaking down matrices into simpler components, spectral decomposition helps reveal the underlying structure of data, making it possible to identify clusters that are not apparent in the original feature space. This article will explore the theory behind spectral decomposition, its role in clustering, and various advanced techniques that utilize this concept.

---

1. Introduction to Spectral Decomposition

1.1 What is Spectral Decomposition?

Spectral decomposition is a process of breaking down a matrix into its constituent components, typically involving eigenvalues and eigenvectors. This technique is fundamental in linear algebra and plays a crucial role in understanding how matrices can be transformed, analyzed, and interpreted.

Linear Algebra and Its Importance:

Linear algebra is the branch of mathematics that deals with vectors, vector spaces, and linear transformations between them. It provides the foundation for many machine learning algorithms, particularly those involving matrices. Spectral decomposition allows us to understand the behavior of a matrix by analyzing its eigenvalues and eigenvectors, which reveal the matrix's intrinsic properties.

1.2 Mathematical Foundation

Given a square matrix $A$, spectral decomposition involves finding its eigenvalues $\lambda$ and corresponding eigenvectors $v$ such that:

$$A v = \lambda v$$

This equation indicates that applying the matrix $A$ to the eigenvector $v$ simply scales $v$ by the eigenvalue $\lambda$. This decomposition is crucial in many applications, including clustering, where it helps identify the directions in which the data varies the most.

---

2. Spectral Decomposition in Clustering

2.1 Laplacian Matrices and Graph Partitioning

One of the most common applications of spectral decomposition in clustering is through the use of the Laplacian matrix in graph partitioning.

2.1.1 Constructing the Laplacian Matrix

The Laplacian matrix $L$ is calculated as:

$$L = D - A$$

where:

• $A$ is the adjacency matrix of the graph (indicating which nodes are connected),
• $D$ is the degree matrix, a diagonal matrix where each entry $D_{ii}$ represents the number of connections (or degree) of node $i$.

The Laplacian matrix captures the structure of the graph, and its eigenvectors can be used to partition the graph into clusters.

2.1.2 Eigenvectors and Graph Partitioning

The eigenvectors of the Laplacian matrix corresponding to the smallest non-zero eigenvalues are particularly important in spectral clustering. These eigenvectors define a lower-dimensional space where the data can be easily clustered using traditional techniques like k-means.

2.2 Modularity in Community Detection

In graph theory, modularity is a metric that quantifies the quality of a network partition into communities. Modularity measures the density of links inside communities compared to links between communities. It is defined as:

$$Q = \frac{1}{2m} \sum_{i,j} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j)$$

where:

• $m$ is the total number of edges,
• $A_{ij}$ is the adjacency matrix,
• $k_i$ and $k_j$ are the degrees of nodes $i$ and $j$,
• $\delta(c_i, c_j)$ is 1 if nodes $i$ and $j$ are in the same community and 0 otherwise.

Maximizing modularity helps identify the optimal division of the network into communities, leveraging the eigenvectors of the Laplacian matrix.

---

3. Practical Applications of Spectral Decomposition in Clustering

3.1 Image Segmentation

Spectral decomposition can be applied to segment images into different regions. By representing an image as a graph where pixels are nodes and edges represent similarities between pixels, spectral clustering can be used to segment the image into distinct regions.

Example of Image Segmentation:

1. Construct a Similarity Graph: Connect pixels that are similar in color or intensity.
2. Compute the Laplacian Matrix: Derive the Laplacian from the similarity graph.
3. Apply Spectral Decomposition: Use the eigenvectors of the Laplacian to cluster the pixels.

This method is particularly effective for images with distinct regions, such as satellite images or medical scans.

3.2 Dimensionality Reduction Techniques (PCA and SVD)

Principal Component Analysis (PCA) and Singular Value Decomposition (SVD) are popular techniques that utilize spectral decomposition for dimensionality reduction.

3.2.1 PCA:

PCA projects data onto the eigenvectors corresponding to the largest eigenvalues of the covariance matrix, capturing the directions of maximum variance. It is particularly useful in clustering to reduce the dimensionality of data, making clusters more apparent.

3.2.2 SVD:

SVD factors a matrix into three components, revealing the singular values and corresponding vectors, which can be used to analyze the structure of the data. SVD is closely related to PCA and is often used interchangeably in applications involving clustering.

3.3 Advanced Techniques

Advanced spectral decomposition techniques include spectral clustering itself, which can be enhanced by methods such as the Lanczos method and Nyström approximation.

• Lanczos Method: An iterative algorithm for approximating the eigenvalues and eigenvectors of large sparse matrices, making spectral clustering computationally feasible.
• Nyström Approximation: A method to approximate the eigenvectors of a large matrix by sampling a subset of the data, allowing spectral clustering to scale to larger datasets.

---

4. Spectral Clustering and K-Means: A Comparative Study

While spectral clustering and k-means are often used together, they differ fundamentally in their approach to clustering.

4.1 K-Means Clustering

K-means clustering partitions data into $k$ clusters by minimizing the variance within each cluster. It assumes that clusters are convex and isotropic, making it less effective for complex cluster shapes.

4.2 Spectral Clustering

Spectral clustering, on the other hand, leverages the eigenvectors of the Laplacian matrix to transform the data into a space where clusters are linearly separable. This allows spectral clustering to detect non-convex and overlapping clusters that k-means might miss.

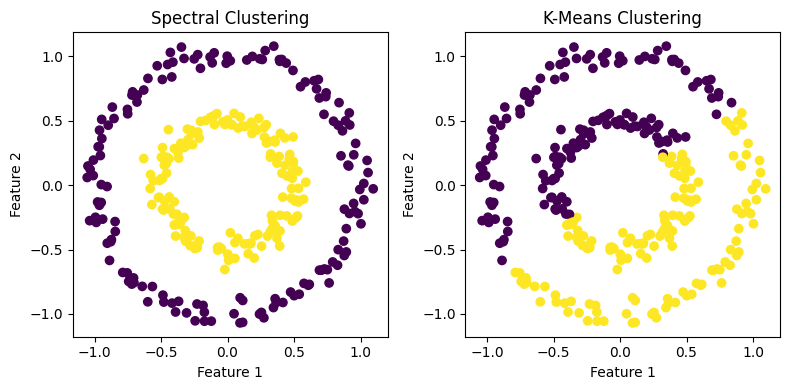
Figure 1: Comparison of Spectral Clustering (left) and K-Means Clustering (right) on a dataset with interlocking circles.

4.3 Comparison and Integration

Example Calculation:

Consider a dataset with two non-convex clusters, such as interlocking circles. K-means would fail to identify the correct clusters, as it relies on Euclidean distance in the original space. Spectral clustering, however, would successfully separate the clusters by projecting the data into a space defined by the eigenvectors of the Laplacian matrix, where the clusters are linearly separable.

---

5. Conclusion

Spectral decomposition is a versatile and powerful tool in clustering, enabling the identification of complex structures within data. By understanding the mathematical foundations and practical applications of spectral decomposition, data scientists can leverage this technique to enhance their clustering analysis, particularly in scenarios where traditional methods fall short.

Key Takeaways:

• Laplacian Matrices: Crucial in graph-based clustering methods like spectral clustering.
• PCA and SVD: Dimensionality reduction techniques that utilize spectral decomposition to simplify clustering tasks.
• Advanced Techniques: Methods like the Lanczos method and Nyström approximation make spectral clustering feasible for large-scale data.