Laplacian Matrices and Graph Partitioning

Laplacian matrices are a fundamental concept in graph theory with significant applications in unsupervised machine learning, particularly in spectral clustering and graph partitioning. This article explores the mathematical foundations of Laplacian matrices, their role in graph partitioning, and their applications in clustering algorithms.

---

1. Introduction to Graphs and Matrices

1.1 Graph Representation

A graph $G = (V, E)$ consists of a set of vertices $V$ (also called nodes) and a set of edges $E$ that connect pairs of vertices. Graphs are widely used in computer science and data science to model relationships and structures in data, such as social networks, molecular structures, and transportation systems.

• Adjacency Matrix: The adjacency matrix $A$ of a graph is a square matrix where each element $A_{ij}$ represents the presence (or weight) of an edge between vertices $i$ and $j$. For an unweighted graph, $A_{ij} = 1$ if there is an edge between $i$ and $j$, and $A_{ij} = 0$ otherwise.

1.2 Degree Matrix

The degree matrix $D$ is a diagonal matrix where each diagonal element $D_{ii}$ represents the degree of vertex $i$, which is the number of edges connected to it:

$$D_{ii} = \sum_{j} A_{ij}$$

The degree matrix plays a critical role in defining the Laplacian matrix of the graph.

---

2. Laplacian Matrices

2.1 Definition of the Laplacian Matrix

The Laplacian matrix $L$ of a graph is defined as:

$$L = D - A$$

Where:

• $D$ is the degree matrix.
• $A$ is the adjacency matrix.

The Laplacian matrix encapsulates the structure of the graph, and its properties are crucial for analyzing the graph’s connectivity and partitioning.

2.2 Properties of the Laplacian Matrix

• Symmetry: The Laplacian matrix is symmetric, i.e., $L = L^\top$.
• Positive Semi-Definiteness: The Laplacian matrix is positive semi-definite, meaning all its eigenvalues are non-negative.
• Eigenvalues and Eigenvectors: The smallest eigenvalue of the Laplacian matrix is always $0$, corresponding to the eigenvector with constant components (often called the trivial eigenvector). The second smallest eigenvalue (the Fiedler value) and its corresponding eigenvector are particularly important for graph partitioning.

2.3 Normalized Laplacian Matrix

In some cases, it is useful to work with the normalized Laplacian matrix, especially when the graph has nodes with varying degrees. There are two common forms of the normalized Laplacian:

1. Symmetric Normalized Laplacian:

   $$L_{\text{sym}} = I - D^{-1/2} A D^{-1/2}$$

2. Random Walk Normalized Laplacian:

   $$L_{\text{rw}} = I - D^{-1} A$$

These normalized forms are particularly useful in spectral clustering, as they adjust for the varying degrees of nodes.

---

3. Graph Partitioning

3.1 The Graph Partitioning Problem

Graph partitioning involves dividing the vertices of a graph into disjoint subsets while minimizing the number of edges between different subsets. This is a critical problem in various applications, such as parallel computing, network analysis, and clustering.

3.2 Min-Cut Problem

One of the classic approaches to graph partitioning is the min-cut problem, which seeks to find a partition that minimizes the total edge weight between different subsets. However, the min-cut approach often results in unbalanced partitions, where one subset is significantly smaller than the other.

3.3 Normalized Cut

To address the limitations of the min-cut, the normalized cut (Ncut) criterion is used, which considers the sizes of the partitions. The normalized cut is defined as:

$$\text{Ncut}(A, B) = \frac{\text{cut}(A, B)}{\text{vol}(A)} + \frac{\text{cut}(A, B)}{\text{vol}(B)}$$

Where:

• $A$ and $B$ are the two partitions of the graph.
• $\text{cut}(A, B)$ is the sum of the edge weights between $A$ and $B$.
• $\text{vol}(A)$ and $\text{vol}(B)$ are the total edge weights connected to the vertices in $A$ and $B$, respectively.

The normalized cut criterion leads to more balanced partitions, making it particularly useful in applications like image segmentation and clustering.

---

4. Spectral Clustering and Laplacian Matrices

4.1 Role of Laplacian in Spectral Clustering

Spectral clustering leverages the eigenvalues and eigenvectors of the Laplacian matrix to perform clustering. The key idea is to use the eigenvectors corresponding to the smallest non-zero eigenvalues to embed the graph's nodes in a lower-dimensional space, where traditional clustering algorithms like k-means can be applied.

4.2 Steps in Spectral Clustering

1. Compute the Laplacian Matrix: Calculate the Laplacian matrix (or normalized Laplacian) for the graph.
2. Eigen Decomposition: Compute the eigenvectors corresponding to the smallest eigenvalues of the Laplacian matrix.
3. Embedding: Use these eigenvectors to embed the nodes into a lower-dimensional space.
4. Clustering: Apply a clustering algorithm, such as k-means, to the embedded points.

4.3 Example: Spectral Clustering on a Simple Graph

Let's consider a simple graph with 6 nodes. The adjacency matrix $A$ is given as:

$$A = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{pmatrix}$$

We then compute the eigenvalues and eigenvectors of $L$. The eigenvectors corresponding to the smallest non-zero eigenvalues can be used to partition the graph into clusters.

Visual Example: Here’s a visual representation of the clustering result.

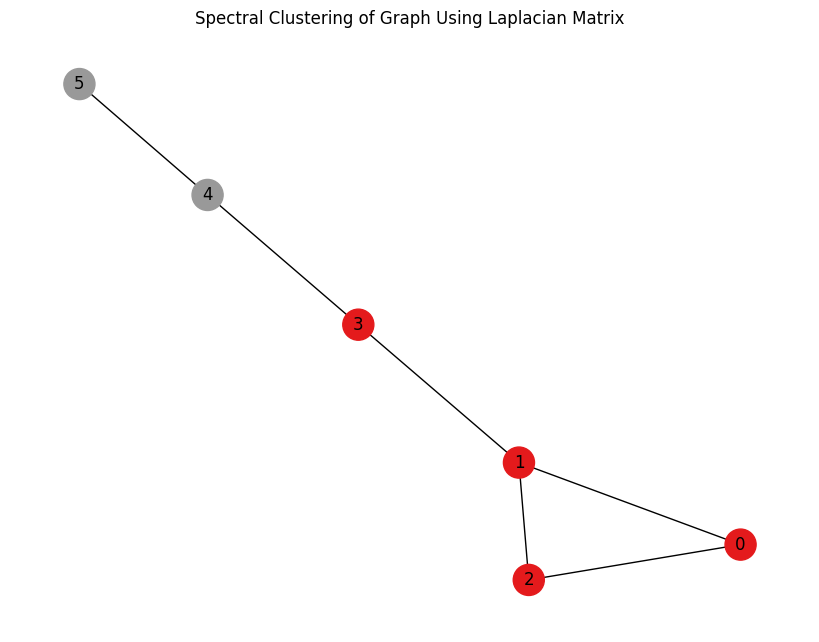
Figure 1: Spectral Clustering of a Simple Graph Using the Laplacian Matrix.

---

5. Applications of Laplacian Matrices in Clustering

5.1 Image Segmentation

Laplacian matrices are widely used in image segmentation tasks, where an image is treated as a graph. Spectral clustering can be applied to segment the image into different regions based on pixel similarities.

5.2 Community Detection in Networks

In social network analysis, communities within networks are identified by partitioning the graph into subgraphs. Spectral clustering, using the Laplacian matrix, effectively detects these communities based on connectivity patterns.

5.3 Dimensionality Reduction

The eigenvectors of the Laplacian matrix can also be used for dimensionality reduction in clustering. By projecting data points onto a lower-dimensional space defined by these eigenvectors, clusters can become more distinct and easier to identify.

---

6. Challenges and Considerations

6.1 Choice of Similarity Measure

The construction of the similarity matrix $A$ significantly impacts the performance of spectral clustering. The choice of the similarity measure (e.g., Gaussian kernel, cosine similarity) and parameters (e.g., $\sigma$ in the Gaussian kernel) should be carefully considered.

6.2 Computational Complexity

Computing the eigenvalues and eigenvectors of the Laplacian matrix can be computationally expensive, especially for large graphs. Efficient algorithms and approximations are necessary for handling large-scale datasets.

6.3 Number of Clusters

Determining the number of clusters is a common challenge in spectral clustering. Techniques such as the eigenvalue gap heuristic can be used, but they are not foolproof. Cross-validation and domain knowledge may also be required.

---

7. Conclusion

Laplacian matrices play a crucial role in graph partitioning and spectral clustering, providing a powerful tool for identifying clusters and community structures in complex datasets. Understanding the properties of Laplacian matrices and how they can be used to transform data for clustering is essential for applying these techniques effectively in unsupervised machine learning.

By leveraging the spectral properties of the Laplacian matrix, spectral clustering offers a flexible and robust approach to clustering, capable of handling non-convex clusters and complex data structures. However, careful consideration of similarity measures, computational resources, and the number of clusters is necessary to achieve optimal results.