Eigenvectors and Eigenvalues in Clustering

Eigenvectors and eigenvalues are fundamental concepts in linear algebra with wide-ranging applications in data science, particularly in clustering algorithms. Understanding these concepts is crucial for leveraging advanced clustering techniques, such as spectral clustering, which rely on the properties of eigenvectors and eigenvalues to discover complex structures in data.

---

1. Introduction to Eigenvectors and Eigenvalues

1.1 What are Eigenvectors and Eigenvalues?

Given a square matrix $A$, an eigenvector $\mathbf{v}$ is a non-zero vector that, when multiplied by $A$, results in a vector that is a scalar multiple of $\mathbf{v}$. The scalar is known as the eigenvalue $\lambda$. Mathematically, this relationship is expressed as:

$$A \mathbf{v} = \lambda \mathbf{v}$$

Where:

• $\mathbf{v}$ is the eigenvector.
• $\lambda$ is the eigenvalue.
• $A$ is the square matrix.

1.2 Geometric Interpretation

Geometrically, eigenvectors represent directions in the vector space that remain unchanged under the linear transformation defined by the matrix $A$. The corresponding eigenvalues indicate how much the eigenvectors are stretched or compressed along these directions.

1.3 Computing Eigenvectors and Eigenvalues

To compute the eigenvectors and eigenvalues of a matrix $A$, we solve the characteristic equation:

$$\text{det}(A - \lambda I) = 0$$

Where $I$ is the identity matrix of the same dimension as $A$, and $\text{det}$ denotes the determinant. Solving this equation yields the eigenvalues $\lambda$. Once the eigenvalues are known, the eigenvectors $\mathbf{v}$ can be found by solving the equation $(A - \lambda I)\mathbf{v} = 0$ for each eigenvalue $\lambda$.

---

2. Role of Eigenvectors and Eigenvalues in Clustering

2.1 Spectral Clustering

Spectral clustering leverages the properties of eigenvectors and eigenvalues to perform clustering on complex datasets. Unlike traditional clustering methods like k-means, which rely on distance metrics in the original feature space, spectral clustering uses the eigenvectors of a similarity matrix (often a Laplacian matrix) to identify clusters.

2.1.1 Constructing the Similarity Matrix

The first step in spectral clustering is constructing a similarity matrix $W$, where each element $W_{ij}$ represents the similarity between data points $i$ and $j$. This matrix is often constructed using a Gaussian (RBF) kernel:

$$W_{ij} = \exp\left(-\frac{\|x_i - x_j\|^2}{2\sigma^2}\right)$$

Where $\sigma$ is a scaling parameter that controls the width of the kernel.

2.1.2 Laplacian Matrix and Its Eigenvectors

From the similarity matrix $W$, we compute the degree matrix $D$, a diagonal matrix where each diagonal element $D_{ii}$ is the sum of the corresponding row in $W$:

$$D_{ii} = \sum_{j} W_{ij}$$

The Laplacian matrix $L$ is then defined as:

$$L = D - W$$

Alternatively, the normalized Laplacian can be used:

$$L_{\text{sym}} = D^{-1/2} L D^{-1/2} = I - D^{-1/2} W D^{-1/2}$$

The eigenvectors of the Laplacian matrix $L$ contain information about the structure of the data. By computing the eigenvectors corresponding to the smallest eigenvalues of $L$, we can project the data into a lower-dimensional space where clusters become more apparent.

2.2 Steps in Spectral Clustering

1. Construct the Similarity Matrix: Calculate the similarity matrix $W$ based on the input data.
2. Compute the Laplacian Matrix: Derive the Laplacian matrix $L$ from the similarity matrix.
3. Find Eigenvectors: Compute the eigenvectors corresponding to the smallest non-zero eigenvalues of the normalized Laplacian matrix (either $L_{\text{sym}}$ or $L_{\text{rw}}$).
4. Cluster in Lower-Dimensional Space: Use a traditional clustering algorithm (e.g., k-means) on the rows of the matrix formed by the selected eigenvectors to identify clusters.

2.3 Practical Example of Spectral Clustering

To visualize how eigenvectors and eigenvalues are used in spectral clustering, consider a dataset with two interlocking circles—a classic example where traditional clustering algorithms like k-means fail to identify the underlying structure.

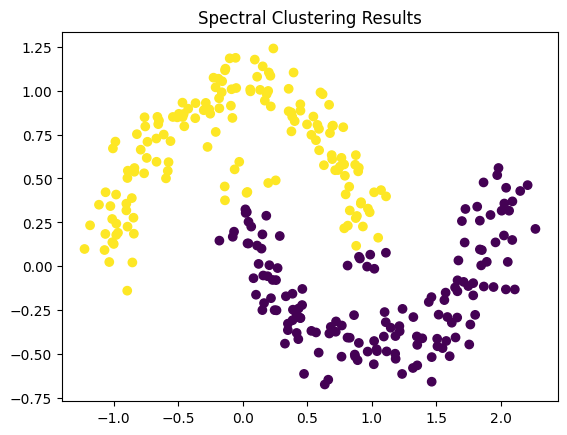
Figure 1: Spectral Clustering Visualization - This image shows the result of applying spectral clustering to a dataset using eigenvectors of the Laplacian matrix, revealing the underlying cluster structure.

In this example, spectral clustering successfully separates the two interlocking circles by transforming the data into a space where the clusters are linearly separable.

2.4 Comparing Spectral Clustering with Traditional Methods

Spectral clustering can detect non-convex clusters that traditional methods like k-means might miss. This is particularly useful in datasets where clusters have complex shapes or are not well-separated in the original feature space.

• K-Means Clustering:
  • Assumptions: Assumes clusters are convex and isotropic.
  • Limitations: Struggles with non-convex or overlapping clusters.
• Spectral Clustering:
  • Assumptions: Relies on the connectivity and similarity structure of data.
  • Advantages: Capable of identifying clusters with complex shapes and varying densities.

Example Comparison: In a dataset with concentric circles or intertwined shapes, k-means would typically fail to separate the clusters accurately, whereas spectral clustering would excel by leveraging the eigenvectors to uncover the intrinsic structure.

---

3. Mathematical Foundations

3.1 Orthogonality and Symmetry

For symmetric matrices $A$, eigenvectors corresponding to distinct eigenvalues are orthogonal. This property simplifies computations and ensures stability in algorithms like spectral clustering.

3.2 The Laplacian Matrix and Its Spectrum

The spectrum (set of eigenvalues) of the Laplacian matrix provides insights into the graph's connectivity and cluster structure.

• Algebraic Connectivity: The second smallest eigenvalue (known as the Fiedler value) measures the graph's connectivity. A higher Fiedler value indicates a more connected graph.
• Eigenvalue Gap: A significant gap between consecutive eigenvalues can suggest a natural number of clusters in the data.

3.3 Relationship with Graph Theory

Spectral clustering is inherently linked to graph theory. By representing data points as nodes in a graph and similarities as edges, eigenvectors and eigenvalues of the graph's Laplacian matrix reveal community structures and cluster memberships.

---

4. Advanced Topics and Variants

4.1 Normalized Spectral Clustering

Normalized spectral clustering involves normalizing the Laplacian matrix to improve the algorithm's performance, especially in cases where clusters vary in size.

• Symmetric Normalization: $L_{\text{sym}} = I - D^{-1/2} W D^{-1/2}$

• Random Walk Normalization: $L_{\text{rw}} = D^{-1} L = I - D^{-1} W$

4.2 Choosing the Number of Clusters

Selecting the appropriate number of clusters $k$ is critical in spectral clustering. Common methods include:

• Eigenvalue Gap Heuristic: Identifying a significant gap in the eigenvalue spectrum to determine $k$.
• Silhouette Analysis: Evaluating clustering quality for different $k$ values.

4.3 Scalability and Computational Complexity

Spectral clustering can be computationally intensive, particularly for large datasets. Techniques like Nyström approximation, sparse similarity matrices, and parallel computing can help mitigate these challenges.

---

5. Conclusion

Eigenvectors and eigenvalues are powerful tools in clustering, enabling advanced techniques like spectral clustering to uncover complex data structures. By understanding the role of these concepts in clustering algorithms, you can apply them effectively to a wide range of data science problems.

Spectral clustering's ability to handle non-convex and overlapping clusters makes it invaluable for diverse applications, from image segmentation to community detection in networks.