Skip to main content

Multidimensional Scaling (MDS)

Multidimensional Scaling (MDS) is a powerful technique used in data science to visualize the structure of high-dimensional data by reducing its dimensionality. MDS helps in uncovering the underlying patterns in data by mapping high-dimensional points into a lower-dimensional space, often two or three dimensions, while preserving the pairwise distances between points as much as possible.

1. Introduction to Multidimensional Scaling (MDS)​

1.1 What is Multidimensional Scaling?​

Multidimensional Scaling (MDS) is a group of techniques used to analyze similarity or dissimilarity data. The goal of MDS is to represent data points in a low-dimensional space such that the distances between the points in this space match the original dissimilarities as closely as possible. This technique is particularly useful in visualizing high-dimensional data.

1.2 Types of MDS​

MDS can be broadly categorized into two types:

  • Metric MDS: Assumes that the dissimilarities between pairs of items are quantitative and attempts to preserve these distances in the low-dimensional representation. Metric MDS tries to maintain the actual distance relationships (e.g., Euclidean distances) between points.

  • Non-metric MDS: Focuses on preserving the rank order of the dissimilarities rather than their exact values. Non-metric MDS is useful when the data only provides information about the order of similarities or dissimilarities, rather than exact distances.

1.3 Applications of MDS​

MDS is widely used in various fields, including:

  • Psychology: To explore the perceptions and preferences of individuals based on pairwise comparisons.
  • Biology: For visualizing genetic distances between species or populations.
  • Marketing: To map customer preferences and perceptions of different products.
  • Social Sciences: To analyze and visualize social networks or survey data.

2. Mathematical Foundation of MDS​

2.1 Dissimilarity Matrix​

MDS starts with a dissimilarity matrix DD, where each element DijD_{ij} represents the dissimilarity between points ii and jj. The dissimilarities can be derived from various measures, such as Euclidean distance, correlation, or other domain-specific metrics.

2.2 The MDS Algorithm​

The goal of MDS is to find a set of points X1,X2,…,Xn\mathbf{X}_1, \mathbf{X}_2, \dots, \mathbf{X}_n in a lower-dimensional space (e.g., 2D or 3D) such that the distances between these points are as close as possible to the dissimilarities in DD.

Steps in Metric MDS:​

  1. Initialize the points in the lower-dimensional space randomly or using another method like PCA.
  2. Compute the distances between all pairs of points in the current configuration.
  3. Compare these distances to the original dissimilarities and compute a stress function that quantifies the difference between them.
  4. Iteratively adjust the points to minimize the stress function, typically using gradient descent or another optimization algorithm.
  5. Converge when the stress function reaches a minimum or falls below a predefined threshold.

Stress Function:​

The most commonly used stress function in MDS is Kruskal’s stress formula:

Stress=∑i<j(dij−d^ij)2∑i<jdij2\text{Stress} = \sqrt{\frac{\sum_{i<j} \left( d_{ij} - \hat{d}_{ij} \right)^2}{\sum_{i<j} d_{ij}^2}}

Where:

  • dijd_{ij} is the dissimilarity between points ii and jj in the original data.
  • d^ij\hat{d}_{ij} is the distance between points ii and jj in the MDS configuration.

2.3 Non-metric MDS​

Non-metric MDS, on the other hand, focuses on preserving the rank order of the dissimilarities. It uses an iterative procedure to find a monotonic relationship between the dissimilarities and the distances in the lower-dimensional space.

In non-metric MDS, the stress function is defined similarly, but it compares the ranks of the dissimilarities rather than their actual values.

3. Practical Example of MDS​

Let’s consider a practical example where we apply MDS to a set of points representing different cities, where the dissimilarity matrix is based on the pairwise distances between these cities.

3.1 Example Data​

Assume we have five cities, and the dissimilarity matrix DD is given by:

D=(010203040100152535201501020302510015403520150)D = \begin{pmatrix} 0 & 10 & 20 & 30 & 40 \\ 10 & 0 & 15 & 25 & 35 \\ 20 & 15 & 0 & 10 & 20 \\ 30 & 25 & 10 & 0 & 15 \\ 40 & 35 & 20 & 15 & 0 \end{pmatrix}

3.2 Visualization​

After applying MDS, we obtain a 2D plot where each point represents a city, and the distances between the points approximate the original dissimilarities.

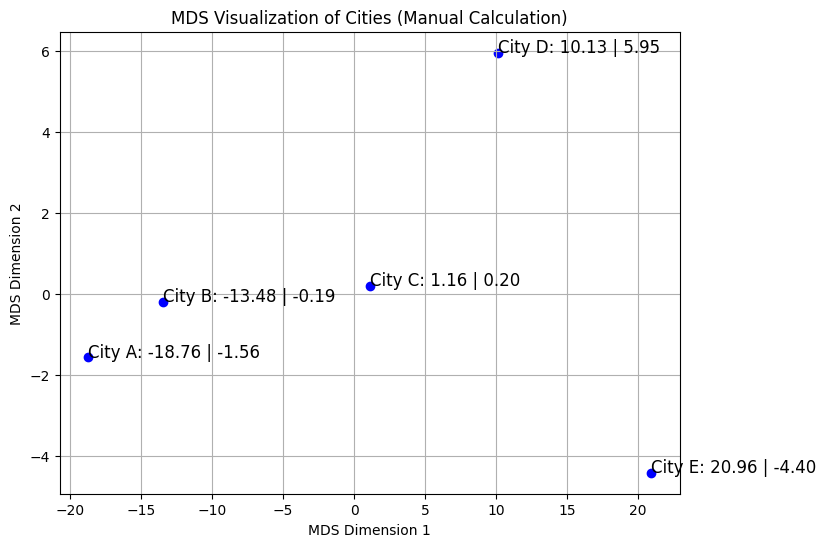
MDS Visualization of Cities

Figure 1: MDS Visualization of Cities - A 2D plot representing the relative distances between five cities.

3.4: Example Calculation in Numpy:​

import numpy as np

# Step 1: Define the Dissimilarity Matrix
D = np.array([
    [0, 10, 20, 30, 40],
    [10, 0, 15, 25, 35],
    [20, 15, 0, 10, 20],
    [30, 25, 10, 0, 15],
    [40, 35, 20, 15, 0]
])

# Step 2: Double Centering

# Compute D^2
D_squared = np.square(D)

# Compute the centering matrix J
n = D.shape[0]
J = np.eye(n) - np.ones((n, n)) / n

# Apply double centering to compute B
B = -0.5 * np.dot(np.dot(J, D_squared), J)

print("D^2 (Squared Dissimilarity Matrix):")
print(D_squared)
print("\nCentering Matrix J:")
print(J)
print("\nDouble Centered Matrix B:")
print(B)

# Step 3: Eigenvalue Decomposition
eigenvalues, eigenvectors = np.linalg.eigh(B)

# Sort eigenvalues and eigenvectors in descending order
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]

print("\nEigenvalues (sorted):")
print(eigenvalues)
print("\nEigenvectors (sorted):")
print(eigenvectors)

# Step 4: Construct the Low-Dimensional Embedding

# Select the first two eigenvalues and corresponding eigenvectors
selected_eigenvectors = eigenvectors[:, :2]
selected_eigenvalues = np.diag(np.sqrt(eigenvalues[:2]))

# Compute the 2D embedding
X = np.dot(selected_eigenvectors, selected_eigenvalues)

print("\n2D coordinates for visualization:")
print(X)

4. Applications of MDS in Data Science​

4.1 Visualization of High-Dimensional Data​

MDS is extensively used to visualize high-dimensional data in a 2D or 3D space. By preserving the dissimilarities between data points, MDS helps in understanding the structure and relationships in the data that are not easily interpretable in high dimensions.

4.2 Analysis of Proximity Data​

In marketing, MDS is applied to understand consumer preferences by analyzing proximity data, such as customer ratings or product similarities. It helps in visualizing how consumers perceive different products relative to each other.

4.3 Genomic Data Analysis​

In bioinformatics, MDS is used to visualize the genetic distances between different species or populations. This helps in identifying patterns of genetic similarity and divergence across species.

4.4 Social Network Analysis​

MDS can also be applied in social network analysis to visualize the relationships and interactions between individuals or groups, providing insights into the structure and dynamics of social networks.

5. Practical Considerations​

5.1 Choosing the Dimensionality​

The choice of target dimensionality (typically 2D or 3D) is crucial in MDS. While lower dimensions are easier to visualize, they may not capture all the variability in the data. Higher-dimensional embeddings can provide a more accurate representation but are harder to interpret and visualize.

5.2 Stress and Goodness-of-Fit​

The stress value is a key measure of the goodness-of-fit in MDS. A lower stress value indicates a better fit, meaning the low-dimensional representation accurately reflects the original dissimilarities. However, stress should be interpreted cautiously, especially in non-metric MDS, where the focus is on preserving rank order rather than exact distances.

5.3 Non-Euclidean Data​

While MDS is commonly applied to Euclidean distance matrices, it can also be used with non-Euclidean data, provided the dissimilarities are meaningful. In such cases, the interpretation of the MDS plot should consider the nature of the underlying dissimilarity measure.

5.4 Computational Complexity​

The computational complexity of MDS increases with the number of data points, making it challenging to apply to very large datasets. Approximation techniques, such as Landmark MDS, can be used to scale MDS to larger datasets by selecting a subset of representative points.

6. Conclusion​

Multidimensional Scaling (MDS) is a versatile and powerful technique for visualizing high-dimensional data in a low-dimensional space. By preserving the dissimilarities between data points, MDS provides insights into the underlying structure of the data, making it an essential tool in data science and exploratory data analysis.

Key Takeaways:

  • Understanding MDS: MDS is used to represent high-dimensional data in a low-dimensional space while preserving the dissimilarities between data points.
  • Applications: MDS is widely applied in fields such as psychology, biology, marketing, and social sciences for visualizing and understanding complex relationships.
  • Practical Considerations: The choice of dimensionality, interpretation of stress, and computational efficiency are key factors in effectively applying MDS.