Skip to main content

Singular Value Decomposition (SVD) for Clustering

Singular Value Decomposition (SVD) is a powerful linear algebra technique used in various data science applications, including clustering. While it shares similarities with Principal Component Analysis (PCA), SVD offers unique advantages, particularly in handling data that is not necessarily centered. This article will delve into how SVD is applied in clustering, provide a comparison with PCA, and present a practical example.

For a comprehensive understanding of SVD's mathematical foundations, please refer to our detailed article Singular Value Decomposition (SVD).

1. Introduction to Singular Value Decomposition (SVD)​

1.1 What is SVD?​

Singular Value Decomposition (SVD) is a factorization technique for matrices, breaking down a matrix AA into three simpler matrices:

A=UΣVTA = U \Sigma V^T
  • UU: An orthogonal matrix representing the left singular vectors.
  • Σ\Sigma: A diagonal matrix containing the singular values.
  • VTV^T: The transpose of an orthogonal matrix representing the right singular vectors.

This decomposition allows us to analyze the structure of the data, reduce its dimensionality, and enhance clustering performance.

1.2 The Role of SVD in Clustering​

In clustering, SVD is used to transform the original data into a lower-dimensional space, where clusters can be more easily identified. By retaining only the most significant singular values, SVD reduces noise and highlights the underlying structure of the data, making it easier for clustering algorithms to operate effectively.

2. Applying SVD in Clustering​

2.1 SVD vs. PCA for Clustering​

While both SVD and PCA are used for dimensionality reduction, they differ in their approaches:

  • PCA centers the data by subtracting the mean before applying the transformation. It is primarily concerned with maximizing the variance in the data.
  • SVD does not require centering and directly decomposes the original data matrix. This makes SVD more flexible in certain applications, especially when the data is not centered.

In clustering, both techniques can be used to reduce dimensionality, but SVD might be preferred when the original data matrix is sparse or when centering is not desired.

2.2 Mathematical Foundation of SVD in Clustering​

Given a data matrix XX with dimensions m×nm \times n, where mm represents the samples and nn the features, SVD decomposes XX as follows:

X=UΣVTX = U \Sigma V^T

Here:

  • UU (size m×mm \times m): Contains the left singular vectors.
  • Σ\Sigma (size m×nm \times n): Contains the singular values along the diagonal.
  • VTV^T (size n×nn \times n): Contains the right singular vectors.

The key idea in applying SVD for clustering is to reduce the dimensionality by selecting only the top kk singular values and corresponding vectors. This reduces the matrix XX to a lower-dimensional representation, where clustering algorithms like k-means can be applied more effectively.

2.3 Steps to Apply SVD in Clustering​

  1. Compute SVD: Decompose the data matrix XX into UΣVTU \Sigma V^T.
  2. Select Top kk Components: Choose the top kk singular values from Σ\Sigma and corresponding vectors from UU and VTV^T.
  3. Transform the Data: Project the original data onto the reduced space formed by the top kk singular vectors.
  4. Apply Clustering: Use a clustering algorithm (e.g., k-means) on the transformed data.

2.4 Practical Example of SVD in Clustering​

Let’s visualize how SVD helps in clustering by transforming a high-dimensional dataset into a lower-dimensional space.

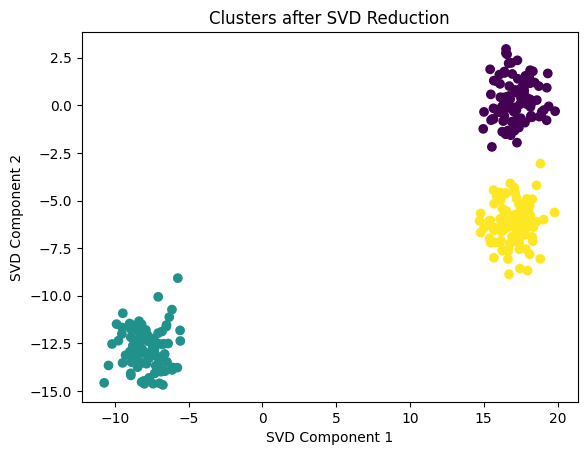
SVD Cluster Visualization

Figure 1: SVD Cluster Visualization - This image shows the result of applying SVD to reduce a high-dimensional dataset, followed by k-means clustering in the reduced space, highlighting the clear separation of clusters.

3. Comparing SVD with PCA for Clustering​

3.1 When to Use SVD over PCA​

  • Non-centered Data: Use SVD when the data is not centered or when the centering step in PCA is undesirable.
  • Sparse Data: SVD is more flexible in handling sparse data, where centering might remove important structural information.
  • Computational Efficiency: In some cases, SVD can be more computationally efficient, particularly when working with large, sparse matrices.

3.2 Performance Comparison​

In general, both PCA and SVD perform well in reducing dimensionality and aiding in clustering. However, the choice between them depends on the specific characteristics of the dataset and the goals of the analysis. PCA is often preferred for datasets where variance maximization is crucial, while SVD is more versatile in handling diverse data structures.

4. Conclusion​

Singular Value Decomposition (SVD) is a versatile tool in clustering, offering flexibility and efficiency, especially for non-centered and sparse data. While it shares similarities with PCA, SVD's unique properties make it particularly useful in certain scenarios. Understanding when to apply SVD over PCA and how to implement it effectively is essential for improving clustering results in various data science applications.

For a deeper understanding of SVD's mathematical foundations, you can refer to our article on Singular Value Decomposition (SVD).